---

The Goldbach Conjecture Creator

On 18 March 1690, the great Prussian mathematician Christian Goldbach was born in Königsberg, Prussia (now Kaliningrad). Although he was a mathematician whose extensive mathematical work is remarkable, what has really made him famous over time has been the correspondence he maintained with the man known in the world of mathematics as ‘the king of mathematics’, that is, the brilliant Swiss mathematician Leonhard Euler, because in this correspondence Goldbach posed the famous mathematical conjecture that to this day remains unsolved and which bears his surname, this is the famous Goldbach Conjecture.

Some consider that Christian Goldbach was not a professional mathematician in the modern sense, but in spite of this, it cannot be denied how immensely important his work is for the backbone of mathematics, i.e. for number theory.

---

Main Mathematical Contributions.

---

• The Goldbach Conjecture:
  Basically, it all starts like this: in a letter sent by Goldbach to Leonhard Euler in 1742, the Prussian mathematician asked him the following two conjectures that are related to each other:

  1. Every even integer greater than 2 can be expressed as the sum of two prime numbers.

  2. Every odd integer greater than 5 can be expressed as the sum of three prime numbers.

  The first of these two conjectures is known as ‘Goldbach's strong conjecture’ or ‘Goldbach's conjecture’ for short, which to this day remains unsolved, and is considered to be one of the central open problems of number theory, and of mathematics in general.

  Regarding the second conjecture, this conjecture is known as the "weak Goldbach conjecture", because if the strong conjecture were proved, this weak conjecture would automatically be proved. It is worth noting that Goldbach's weak conjecture was proved by the Peruvian mathematician Harald Helffgot in 2013, using extensive computing power and statistical tools.

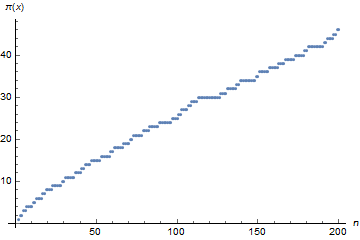
Number of primes (π(x)) less than or equal to 200

---

Life and Performance.

---

Goldbach is known to have been an outstanding student at the University of Königsberg, where he dabbled in other fields of knowledge besides mathematics, such as medicine and law. He was also a great traveller in search of knowledge, travelling extensively throughout the old continent of Europe, where he had the opportunity to meet the great exponents of mathematics of his time: Leonhard Euler, Gottfried Leibniz and even the whole famous scientific and philosophical family of Bernoulli.

In 1725, he moved to Russia, specifically to St. Petersburg, where he established himself as a professor of mathematics, and due to his outstanding work as a teacher he eventually became Secretary of the Academy of Sciences of St. Petersburg, a very important position at the time. As mentioned above, his long-standing correspondence with Euler was fundamental to the development and establishment of number theory in the 18th century.

Key Publications:

• Correspondence with Leonhard Euler :
  Without becoming redundant with all the above, it should always be emphasised that Goldbach's most important mathematical work is contained in all the correspondence he had with Euler over a significant period of time, where, in addition to his two famous conjectures, he also expressed other important mathematical ideas, among which his contributions on the subject of infinite series stand out, a subject that is usually central to the study of number theory and the study of the properties of prime numbers.

• Work on Infinite Series:
  Here are two of his most important works in Infinite Series
  1. 'De transformacióne serierum' ( (1729)
  2. 'De terminis generalibus serierum' (1732).

  Although his work is generally lacking in length, his weight in number theory has been undeniable and has helped to advance research in this area of mathematics.

---

It is important to mention the special importance that communication by correspondence had for mathematicians in the 18th century, since it was through this that new ideas in mathematics were disseminated among their colleagues, so that through such correspondence the advancement of research in different areas of mathematics was often achieved, It can be said that the work of Professor Christian Goldbach, especially with all the mathematical development in number theory that occurred after the statement of his two famous conjectures, was carried out by numerous mathematicians working with the aim of answering these conjectures related to the basic blocks of mathematics, which are prime numbers.

The Professor Goldbach passed away in Moscow, the capital of Russia, on November 20, 1764.

Today we can see how Christian Goldbach's work has even driven the development of computer technology, where computer tests have been carried out to find prime numbers that do or do not satisfy his famous conjecture, even going so far as to search in integers of the order of 10¹⁸, which justifies the use of immense computing power.

Note: Even if the search for primes goes up to 10¹⁸, since the set of integers is an infinite set, this is only an infinitesimal part of the set, ergo these calculations don't count as a formal proof.

Note II: A prize of over a million dollars is currently being offered for proving or disproving Goldbach's conjecture.

Thank you very much for your invaluable contribution to mathematics, Professor Goldbach.

Some of His Contributions.

---

---

---

---

Christian Goldbach Portrait Image Source

---

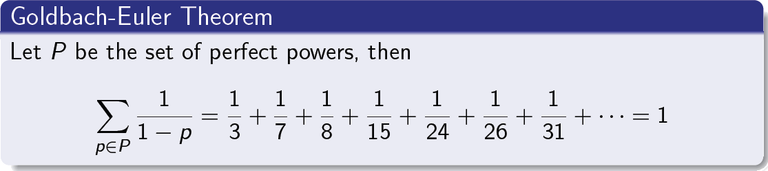
Note: All the images related to Goldbach Contributions are crafted by me using the text editor based on LaTeX: Beamer. Also, the plot about the primes distribution shown in this post were created by me using the Wolfram language: 'Mathematica'.

'The Structure of this article is by my authorship too.'

Regards.

---

References

Weisstein, Eric W. "Goldbach Conjecture." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/GoldbachConjecture.html

Helfgott, Harald A. (2013). "The ternary Goldbach conjecture is true". arXiv:1312.7748 [math.NT].

The Goldbach-Euler Theorem. (2022, 26 de septiembre). Maths Feed Blog. https://mathsfeedblog.wordpress.com/2022/09/26/the-goldbach-euler-theorem/

---

---